Breaking Sticks

This post is based on a probability puzzle. What is the probability that breaking a straight stick at 2 random points will result in 3 segments that can form a triangle.

Consider the resulting segment lengths: , . Let the stick length =1.

Now,

To form a triangle

for all

These constraints reduce to:

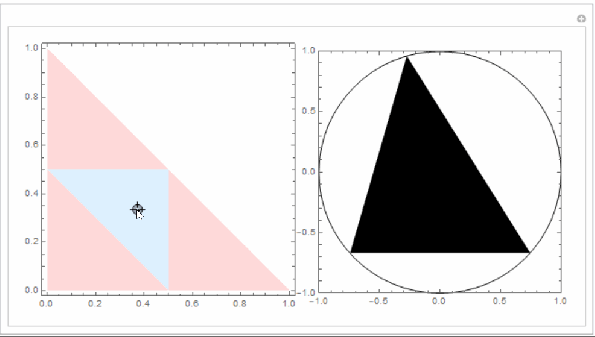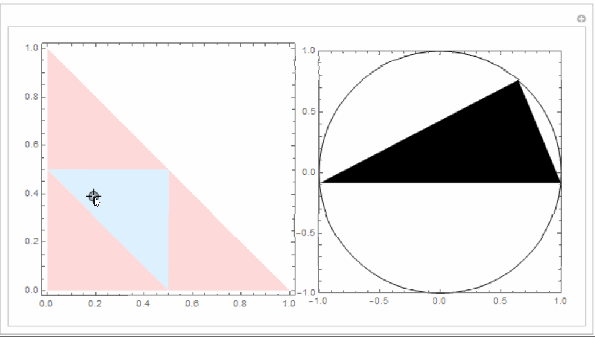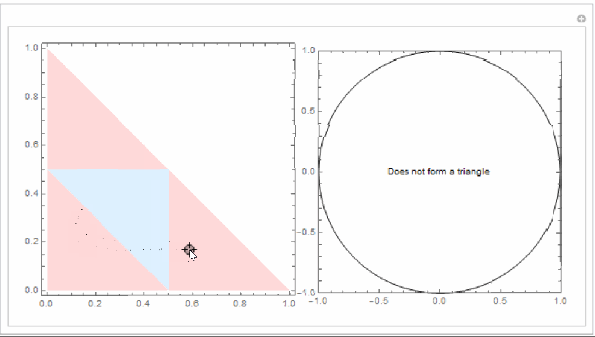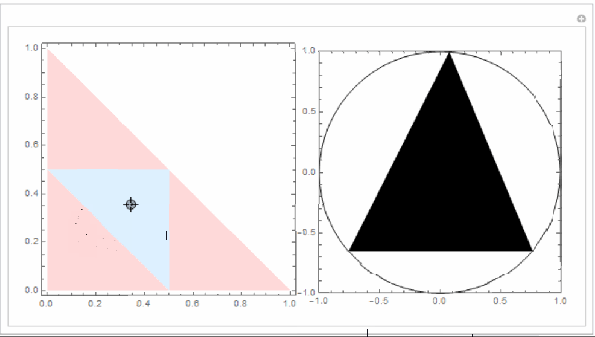
You can visualize this as follows. As there are only 2 degrees of freedom, consider only space of . The space of allowable is the region of the unit square: . Within this space the values of that form a triangle with lengths is the region satisfying the constraint above.

The probability is then: (1/8)/(1/2)=1/4.

 

Just for fun:

 

 

The light blue triangle is the region of that can form triangle and the pink triangle encloses the allowable stick segments.

The triangles on the right have been rescaled to be circumscribed by the unit circle. The relative lengths pertain not the absolute lengths.